Function Printing
There are various possibilities to alter the vertex positions by mathematical functions.
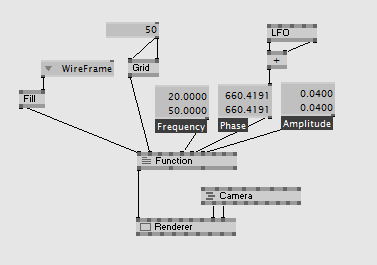
For the following examples we use a Grid (EX9.Geometry) as input. Set the resolution to about 50x50.
f(x, y) = z
Create a new z coordinate by x and y. Using the MrWiggle example we could write:
float2 Frequency = 10;
float2 Phase = 0;
float2 Amplitude = 0.01;
vs2ps VS(
float4 PosO : POSITION,
float4 TexCd : TEXCOORD0)
{
//declare output struct
vs2ps Out;
//calculate two waves
float2 wave = sin(PosO.xy * Frequency + Phase) * Amplitude;
//set z coordinate
PosO.z = wave.x + wave.y;
//transform position
Out.Pos = mul(PosO, tWVP);
//transform texturecoordinates
Out.TexCd = mul(TexCd, tTex);
return Out;
}
using a patch like:
f(u, v) = xyz
Another common type is to calculate a completely new position from the xy coordinates of the grid. This is often called parametric surfaces, where the xy input parameters are called uv.
for example a cone:
x = v*cos(u)
y = v*sin(u)
z = v
can be written as a function:
float3 Cone(float2 uv)
{
float u = uv.x;
float v = uv.y;
float3 newPos;
newPos.x = v * cos(u);
newPos.y = v * sin(u);
newPos.z = v;
return newPos;
}
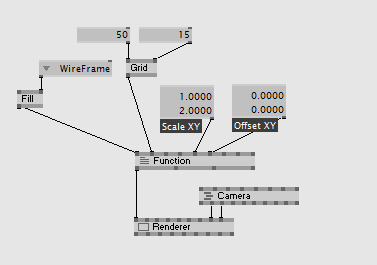
It might be handy to scale u by two pi to get a full cycle in the range 0..1, as well as have a general offset and scale for the input parameters. The vertex shader could then look like:
1. define twopi 6.28318531
float2 Scale = 1;
float2 Offset = 0;
float3 Cone(float2 uv)
{
uv *= Scale;
uv += Offset;
float u = uv.x * twopi;
float v = uv.y;
float3 newPos;
newPos.x = v * cos(u);
newPos.y = v * sin(u);
newPos.z = v;
return newPos;
}
vs2ps VS(
float4 PosO : POSITION,
float4 TexCd : TEXCOORD0)
{
//declare output struct
vs2ps Out;
//set new position
PosO.xyz = Cone(PosO.xy);
//transform position
Out.Pos = mul(PosO, tWVP);
//transform texturecoordinates
Out.TexCd = mul(TexCd, tTex);
return Out;
}
And the patch:
Next: Vertex Data
Back: Mr. Wiggle
TOC: ((Tutorial - Of Effects and Shaders|Of Effects and Shaders))
